Palavras chave:
forma diferencial,
forma diferencial exata,
gradiente,
Henri Cartan,
jacobiana,
teorema da Divergência de Gauss (citação)
teorema de Green
teorema de Stokes (citação)

O Teorema de Green
É o objetivo da lista 06.
É um dos teoremas mais bonitos da história recente da Matemática, não vou refazer aqui a história que
você pode encontrar em diversas páginas na Internet e @ aconselho a fazer esta busca, mas tente não
se perder na riqueza de detalhes que você irá encontrar.
É possível que que alguém discorde de mim (coisa fácil), mas eu costumo dizer
que Henri Cartan, que morreu
há dois anos com 104 anos de idade, dedicou a sua vida a esclarecer o
Teorema de Greeen e mais dois outros
teoremas que representam o mesmo que este teorema com ligeiras
diferenças na sua apresentação, o Teorema de
Stokes e o Teorema da Divergência de Gauss.
Eles são uma formulação sofisticada do Teorema Fundamental do
Cálculo Integral no sentido de que relacionam duas integrais, uma em dimensão n e
a outra em dimensão n-1,
analise esta fórmula
que se encontra ao final da lista 06.
-
O Teorema Fundamental do Cálculo "reduz" o cálculo da uma integral à variação da primitiva ao
longo do intervalo
o que é feito calculando os valores da primitiva na fronteira do intervalo que é um
domínio de dimensão zero (dois pontos)
ao passo que a integral da função é sua variação ao longo de um domínio de dimensão 1,
um intervalo.
Transforma assim uma integral sobre um domínio de dimensão 1 numa
outra integral sobre um domínio de dimensão zero.
- O teorema de Green faz o mesmo, avalia a integral de uma função
sobre um domínio do plano (dimensão 2) usando uma
integral de linha (integral sobre um domínio de dimensão 1).
- É o mesmo que fazem os dois outrso teoremas, de Stokes
e da divergência (de Gauss), apenas eles estão formulados sobre
variedades que se encontram em espaços de dimensão maior.
Eles são comumente apresentados em espaços de dimensão 3.
Você pode ver exatamente o que eu disse acima
nesta página, ela inclusive começa com o Teorema
Fundamental do Cálculo apresentado de maneira semelhante a que eu descrevi acima.
Para deixar isto claro, que estes quatro teoremas representam praticamente a mesma coisa,
Cartan (e muitos outros que
colaboraram com ele) construiu uma teoria, a teoria da formas diferenciáveis.
P(x,y) dx + Q(x,y) dy
é uma forma diferenciável, 1-forma diferenciável que é a derivada de z = F(x,y) -
notação da lista 06.
Como P(x,y) dx + Q(x,y) dy
é a derivada de
z = F(x,y),
se P = Fx; Q = Fy e você pode concluir que é assim
apenas calculando a derivada implícita de z = F(x,y), então a integral desta
forma diferencial exata (uma derivada, outro nome para a derivada) é zero como
consequência direta do Teorema Fundamental do Cálculo:
F(p) - F(q); p = q;
os dois extremos iguais de uma curva fechada....
O Teorema de Schwartz-Clairaut garante que a integral dupla seja nula, porque como as
derivadas mistas são iguais, então
Qx = Fyx = Fxy = Py
e assim o integrando na integral dupla
Qx - Py
é zero. É necessário apenas alguma vivência com Cálculo à duas variáveis para entender
estes cálculos.
Na lista 06 eu tentei criar um método pedagógico para que se entenda este belo teorema
e consegui apresentá-lo
em sua
forma trivial. Na próxima etapa, lista 07, eu vou mostrar as consequências de eliminar a "trivialidade" nesta formulação
do Teorema de Green que irá abrir um leque significativo de aplicações. Entendido o Teorema de Green os dois outros teoremas
mencionados acima vai ficar bem mais fáceis de serem compreendidos, e se eu tiver sucesso nesta empreitada estarei, com
orgulho, participando com uma pequena contribuição, do projeto de Henri Cartan -
ele sabia o que estava fazendo!
Comentando a lista 06
Vou agora comentar cada uma das questões da lista.
A primeira questão
O objetivo da primeira questão é habituá-l@ com o uso de integrais de linha, que é uma das
expressões do Teorema de Green, é expressão que se encontra à direita
na equação do teorema.
O objetivo aqui é bem simples: treinar o uso de uma parametrização de uma curva e aprender
que o cálculo de uma integral sobre uma curva, a chamada integral de linha, se transforma
numa integral do Cálculo I.
A segunda questão
Na segunda questão temos o cálculo de algumas integrais duplas. Treinar o uso do cálculo de
integrais duplas quando o domínio não é um retângulo.
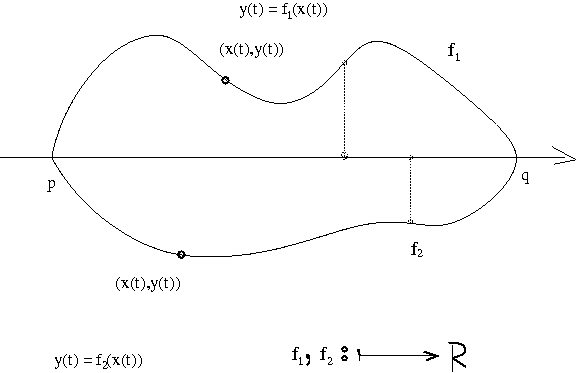
Este gráfico aparece no começo da lista é usado como motivação para o cálculo das integrais
na questão 02.
O domínio D é limitado pelo gráfico de duas funções f1, f2 definidas
no mesmo intervalo [p,q] o que vai fazer com que a integral dupla iterada seja calculada
com uma das integrais sobre o intervalo [p,q] e a outra sobre intervalos variáveis cujos limites
são definidos pelos gráficos das duas funções f1, f2.
A questão 03
A questão 03 encontra motivação no gráfico
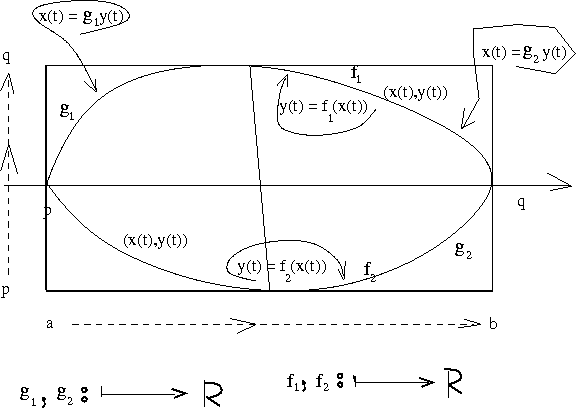
em que o domínio D tanto pode ser visto como variando de f1 para f2 como
de também de g1 para g2.
Nenhum dos dois tipos de domínio é dos mais "complicados" porém, se você se habituar com a
dificuldade que estes dois tipos de domínio oferecem (ou melhor, com as facilidades que eles
oferecem para descrever a variação no cálculo da integral), qualquer outro domínio mais "complicado"
será fácil de entender. Na última questão eu vou usar um domínio mais complicado.
Os cálculos nesta questão vão nos preparar para entender a "demonstração" da forma trivial do
Teorema de Green de que será objeto a próxima questão.
A questão 04 - finalmente o Teorema de Green
É, finalmente chegamos ao Teorema de Green.
Nesta questão, item por item, estamos fazendo as contas que vão nos levar ao item (e) em que
aparece a fórmula do Teorema de Green.
É o caso trivial porque a forma diferencial P(x,y) dx + Q(x,y) dy é a derivada implicita de
z=F(x,y) em que a função F é suposta ser uma função diferenciável. (P Q) é o gradiente de F,
ou ainda, P, Q são as derivadas parciais de F.
Consequentemente F pode ser recuperada a partir de (P, Q) por integração (é a primitiva de
(P,Q) ) de forma semelhante a que se faz no Cálculo I.
Neste caso, dados dois pontos P,Q no plano, calcular a integral de F desde P até Q não depende
do caminho porque quando formos de P até Q e retornamos de Q até P, teremos um caminho fechado
e sobre caminhos fechados a integral de P(x,y) dx + Q(x,y) dy é zero. É o caso trivial do
Teorema de Green, quando ainda se diz que esta integral não depende do caminho, porque
tomados dois caminhos diferentes eles definem uma curva fechada sobre a qual a integral será zero,
a integral tem o mesmo valor, não importa por qual caminho se vá de P até Q.
É isto que caracteriza (ou é caraterizado por...) a derivada de F é (P,Q).
A última questão - 05
Nesta última questão você deve fazer várias aplicações do Teorema de Green calculando
o valor de integrais duplas transformadas em integrais de linha sobre a fronteira do
do domínio de integração.
Pelo menos uma delas o resultado é diferente de zero, portanto
se trata do caso não trivial do Teorema de Green.
Vou discutir melhor isto na próxima lista, porém aqui já estamos encontrando os casos em que
as duas integrais na expressão do Teorema de Green,
são iguais mas não precisam ser zero. Os itens (c) e (e) se completam... com uma diferença de
sinal, e vamos discutir porque tem esta diferença de sinal, estes dois itens dão um exemplo
do caso não trivial do Teorema de Green.
A diferença de sinal vem da orientação que for dada à curva fronteira do domínio. Uma curva pode
ser percorrida de duas formas diferentes, quer dizer que há duas orientações para o cálculo da
integral de linha e você aprendeu que quando se inverte o sentido domínio de integração, em
Cálculo I, a integral troca de sinal.
É o caso aqui entre estes dois itens da questão 05.
Os intens (c) e (e) da questão 05 usam este gráfico

Observe que é um retângulo do qual foi retirado um círculo, portanto é um domínio com um buraco
no seu interior.
A fronteira deste domínio é formada de uma curva que não é conexa, é formada de dois ramos, a
fronteira do losângulo e a fronteira do círculo que foi retirado do losângulo.
No item (e) você
pode acompanhar e verificar se estão corretos os cálculos, da integral de linha em cima desta
fronteira.
Aqui vou discutir "orientação" da fronteira, há duas. Numa das orientações o interior da região fica
sendo apontada pelo vetor normal (aparece o desenho no gráfico). Se a orientação for invertida
o vetor normal irá apontar para fora da região.
Um problema para o qual a fita de Moebius é um exemplo simples: nem toda curva fechada encerra o interior
de uma região... e consequentemente existem superfícies que não podem ser orientadas:
elas não tem nem interior e nem exterior. Vou voltar a discutir isto mais a frente.
Inicialmente vou deixar de lado a possibilidade de existirem superfícies sem orientação possível e vou discutir
como orientar quando isto for possível. Vou usar um exemplo simples que você pode construir a partir da
descrição que vou fazer e, embora simples, é bastante genérico.
O vetor normal é um vetor unitário que é
perpendicular à tangente,

e então é possível haver dois vetores normais,
mas esta
dubiedade desaparece em certos casos:
- Primeiro consideramos uma orientação da fronteira, escolhemos uma forma de percorrer a curva;
esta escolha é arbitrária mas logo você vai ver que há uma escolha a ser feita;
- Escolhida uma orientação para a curva, podemos aplicar o vetor tangente a um ponto da
curva e ele vai estar de acordo com a orientação escolhida, lembre-se do que mostrei
quando discuti porque existe uma orientação positiva para o círculo trigonométrico que
nos permite dizer que os relógios (antigos, de ponteiros, ecológicos) andavam no sentido
negativo;
- Basta calcular a derivada de (cos(t), sin(t)) e levar o vetor derivada para a extremidade
do vetor posição que você encontra a orientação positiva do círculo trigonométrico.
- O vetor normal é calculado usando a regra que você estudou em Física, é o vetor que fizer um
ângulo positivo (no sentido positivo) de 90º graus com o vetor tangente, isto elimina um
dos vetores normais ficando apenas um que é o que chamaremos de vetor normal (o outro é
descartado);
- No caso do círculo trigonométrico podemos recuperar um resultado intrigante do Ensino Médio, que a
orientação positiva do círculo trigonométrico deve ser a inversa da que tinham os relógios de ponteiro.
- Derive a parametrização habitual do círculo: (cos(t), sin(t)) e o resultado será
(-sin(t), cos(t))
o vetor derivada, que é
um vetor perpendicular ao vetor posição, faça o produto escalar para vê-lo.
- Deslise o vetor derivada para a extremidade do vetor do vetor posição, para obter o vetor tangente (a derivada não produze
vetores tangentes);
- Calcule a segunda derivada (derivando a derivada), o resultado é um vetor perpendicular ao vetor derivada. Surpreendente?
é o inverso aditivo do vetor posição, os dois se encontram sobre a mesma reta suporte, mas dirigidos em direções opostas.
Consequentemente o vetor segunda derivada é perpendicular ao vetor derivada. Observe que isto não vai
acontecer com qualquer curva, é típico do círculo. Em equações diferenciais você irá ver que esta
propriedade é a equação diferencial de uma família de círculos.
- Isto não é por acaso! Os gregos consideravam o círculo, a esfera, formas perfeitas e resvalavam para questões místicas
envolvendo as deidades. Se não houver nenhum força atuando,
qualquer corpo tende a adquirir a forma esférica. Você perceber um pouco disco fazendo bolas de sabão! As bolas de
sabão não são exatamente esféricas porque existe uma pequena diferença entre a parte superior e a inferior devido ao peso do
ar, a diferença é pequena, mas a bolha de sabão é muito fraca. Mas são quase esféricas. É a tentativa de todos os corpos
soltos no Universo, tenderem à forma
esférica, o que nem sempre é possível devido a complicações de forças externas ou internas, devido a heterogeneidade do
material de que são feitos os corpos soltos no Universo, o que provoca o surgimento de montanhas por
ou falhas "geológicas". Não fossem estas atrapalhações o corpo seria esférico, é o equilíbrio.
- No caso do círculo (e da esfera) a tangente é perpendicular ao raio e no caso
de um corpo gravitando em torno de outro (se tudo fosse simples) num trajetória circular, o corpo de maior massa age sobre
o corpo de menor massa (que absurdo... matéria atrae matéria...todos os dois agem um sobre o outro, mas vou ficar na visão
externa, que enganou e continua enganando muita gente) a atração da gravidade age ao longo do vetor aceleração - e ela que altera
o movimento do corpo "preso" pela gravitação,
que se não estivesse preso seguiria em trajetória retilínea (movimento uniforme sem aceleração). Se a trajetória fosse circular,
a linha de ação da força de gravidade seria o raio do círculo.
- Como nem tudo é tão simples, os corpos se encontram em trajetórias elípticas (também é falso, não há curvas fechadas
no Universo),
mas continuando com a nossa visão local dentro do nosso sistema solar heliocentríco,
uma distorção da realidade que funciona
razoavelmente, enganou e continua enganando muita gente, a trajetória é elíptica e uma elipse é uma distorção de um círculo,
em vez de ter um centro tem dois focos, e cada ponto na elipse se liga aos dois focos por um segmento de reta. Na verdade a elipse
também é uma parábola distorcida... e a força de gravidade atua sobre a linha que liga o corpo a um dos focos
(o Sol no caso da Terra).
- O caso da elipse serve para provar que o vetor aceleração não precisa ser perpendicular ao vetor derivada,
ou melhor, somente será
no caso excepcional do círculo.
Falei acima que esta dubiedade (do vetor normal) desaparece em certos casos.
Há regiões que não tem
nem exterior e nem interior,
um dos exemplos mais bonitos e simples é a fita de Moebius (o símbolo
do IMPA)
que pode ser construída em papel. Faça
uma busca na internet para descobrir como... é uma superfície que não tem interior
e nem exterior,
e consequentemente fica difícil definir o vetor normal como eu fiz acima.
A escolha de orientação altera o sinal da integral, que é o objetivo na questão 05.
Se uma região tiver interior existe então uma orientação natural para sua fronteira, é aquela em que o vetor normal
aponta para o interior. Esta é a razão da escolha da orientação do círculo que é parte da fronteira da região
considerada nos itens (c) e (e) da questão 05.
Solução do item e - questão 04
Embora estes cálculos sejam um caso particular, um domínio muito bem escolhido, convexo, vamos ver
que nos casos mais gerais será possível decompor o domínio de integração em uma reunião de domínos
convexos e somar os resultados. Então entender bem o que acontece neste caso é um primeiro passo para
entender a demonstração geral deste belo e intrigante teorema.
Sim, o Teorema de Green foi "intrigante"
por muito tempo até que uma teoria adequada o colocou com um item natural na sequência dos resultados
envolvendo integrais múltiplas.
Durante muito tempo ele apenas era uma fórmula que servia para calcular
diferenças de potenciais, ou melhor, defeito num potencial.
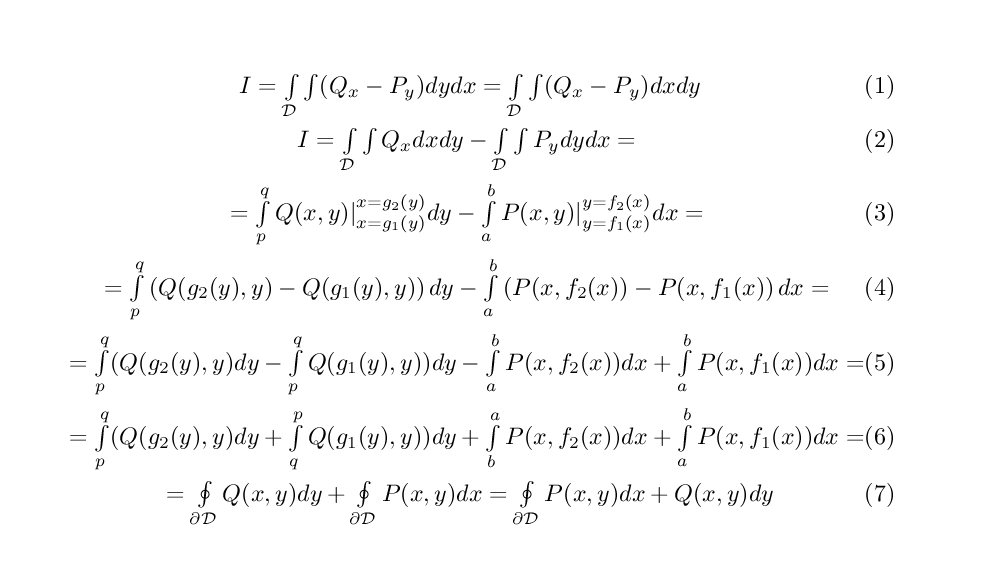
- Na equação (1) estou explicitando que a integral, se existir, pode ser calculada em qualquer ordem, primeiro relativamente a "x"
ou, inversamente, começando com "y". Vou precisar desta propriedade logo na equação (2) para escolher uma forma melhor no
cálculo da integral de Qx ou Py;
- Na equação (2) separei em duas integrais a diferença Qx - Py porque cada uma delas tem uma forma
melhor para ser calculada. Como Qx é a derivada relativamente a "x" então é melhor calcular a integral dupla neste
caso na ordem "dx dy" e reverter a ordem de integração para o caso Py;
- Nas equações (3) e (4) calculei as duas integrais - uma das integrais em cada caso...;
- Na equação (5) separei todos os integrandos, cada um numa integral, para que possamos melhor entender a ordem como a fronteira
vai ser percorrida;
- A integral de Q na equação (6) corresponde a esta figura;

a reversão dos limites de integração permite que a fronteira seja percorrida toda no mesmo sentido.
A integral de P na equação (6) corresponde a esta figura;
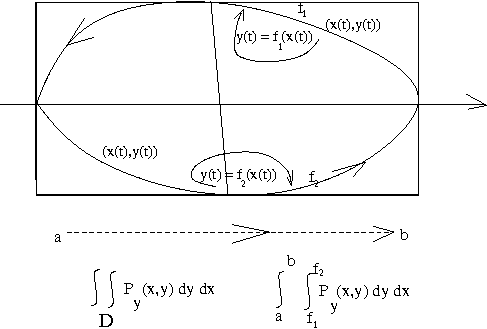
e o sinal diferente de P garante que a reversão dos limites de integração
permita que a fronteira seja percorrida toda no mesmo sentido em que foi feito o percurso na integral anterior.
- Como a fronteira do domínio D é percorrida de forma "sincronizada"
nas duas integrais, de P e de Q é possível escrever uma única integral na equação (7).
- Como eu não usei mais, em nenhum momento que alguma das integrais seja nula, então provei o Teorema de Green,
a igualdade entre as duas integrais quando o domínio é convexo.
- Neste caso, quando o domínio for convexo, podemos ver a fronteira como a união de
dois gráficos de funções definidas no mesmo intervalo, f1, f2 no intervalo [a,b] ou
g1, g1 no intervalo [p,q].
Assim, a forma trivial do Teorema de Green vale no caso não trivial. Quando a integral de linha, no caminho fechado for
diferente de zero, a integral dupla, sobre o domínio, terá o mesmo valor: as duas integrais tem sempre o mesmo valor.
O próximo passo será entender como fazer com domínios quaisquer. Esta é uma forma muito genérica de falar e a demonstração
é muito complicada (apesar de que as contas sejam as mesmas) relativamente a um domínio qualquer. Mas eu vou poder mostrar
que como se faz em domínios bastante complicados. Este vai ser o objetivo das aulas nesta semana que vem, e o texto será
completado para servir de suporte ás aulas. Visite a página para ver a sequência!
Significados do Teorema de Green
Aquilo que se transformou
O teorema de Green
tem diversas aplicações. No início de sua existência, ou talvez a sua existência tenha o que ver com a
interpretação que agora vou dar, ele separava potências entre conservativos ou não conservativos.
É muito possível que tenha sido esta a motivação da descoberta do teorema por Georges Green que teve seus estudos
muito influenciados pela Física e por campo eletro-magnéticos. O teorema de Green explica bem o comportamento destes
campos, ou melhor, é essencial para cálculos com campos eletro-magnéticos.
Mas a expressão do teorema, como se encontra no item da questão 04 apenas faz desta fórmula uma expressão complicada,
liga um campo vetorial (P,Q) às duas derivada parciais. A expressão trivial, quando (P,Q) é a derivada de F, também não
ajuda muito a sua compreensão pelo fato mesmo de que é um caso trivial e aparentemente sem a menor importância.
Ora, é exatamente o caso trivial que é o importante embora não seja ele o predominante no mundo real... quando ele se refere
a um campo conservativo e atendendo a um princípio central da Física - a conservação da energia. Embora a energia se conserve,
não é isto que nós "observamos" no dia-a-dia! O princípio de Lavoisier parece muito longe da realidade: na natureza nada se
cria e nada se perde, tudo se transforma.
A primeira observação que temos é que muito vive se perdendo e que a transformação é muito pequena e muito lenta para enfrentar
o desperdício que fazemos....
Retornando ao Teorema de Green, ele mede o que se transformou de um potencial quando a integral não é zero.
Esta é a grande importância do Teorema de Green para a Física.
A importância do caso trivial
É o caso trivial que é muito importante do ponto de vista teórico, para a Matemática, na verdade uma comparação
entre os dois casos:
- Se (P,Q) satisfizer o caso trivial então (P,Q) = (Fx, Fy) é a derivada de um potencial.
Neste caso dizemos que a integral de linha no teorema
separa os campos vetoriais em dois tipos -
- integrais que dependem de caminhos, quando a integral de linha no teorema for diferente de zero para algum
caminho fechado, ou
- integrais que não dependem de caminhos, quando a integral de linha no teorema for zero para qualquer
caminho fechado.
- Mas esta forma de ver é extremamente complicada! Como é que poderiamos provar que (P,Q) define integrais independente
de caminhos? Na verdade é simples, mas depende de uma idea que não se explica sozinha.... basta calcular as derivadas parciais
Py, Qx
e verificar se são iguais. Ora esta explicação precisa de ver (P,Q) como um gradiente. Durante muito tempo os livros seguiram
por este caminho talvez porque não entendessemos claramente o que acontecia. O conceito "integrais independentes de
caminhos" era um tópico importante.
É aqui que entra o trabalho a que já me referi
de Henri Cartan, ele viu o Teorema de Green (e também o de Stokes e da divergência de Gauss) como um único resultado:
Existem funções vetoriais (P,Q) que são derivadas;
Existem funções vetoriais (P,Q) que não são derivadas;
Estes dois casos representam exatamente a mesma coisa, (P,Q) ser um gradiente ou a
integral de linha de (P,Q) ser independe
de caminhos. Mas isto não parecia claro.
É a outra aplicação do Teorema de Green!
A orientação de uma fronteira não conexa
Um dos problemas que vamos encontrar, nas aplicações do Teorema de Green, é a
existência de domínios com buracos no seu interior.
Uma forma simples de mostrar que
este problema não é uma invenção maquiavélica para tornar a disciplina difícil é
a consideração de funções racionais, aquelas que são frações com polinômios no
numerador e no denominador.
Estas funções servem para modelar, localmente, situações em que há presença de fontes
de energia muito alta (uma conceito relativo....), por exemplo, dois buracos negros que
a distãncia em que nos encontramos "parecem ser vizinhos". A função que serviria para
modelar, localmente a gravidade nesta regão, teria no denominador uma função se anulando
nos pontos geométricos em que ficam os buracos negros, com zeros duplos para seguir a lei
da gravitação universal do quadrado da distância. Quando uma função tem um denominador
com zero, estes se chamam "polos" em oposição ao nome "raizes" para os zeros do numerador.
Não vou estudar a astronomia desta questão, estou apenas usando o exemplo astronômico como
motivação para a existência do problema.
O domínio desta função teria
que ter estes pontos retirados. A 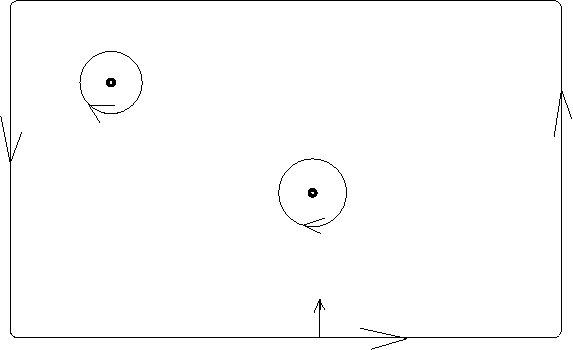 figura ilustra de modo "plano" uma região do Universo
em que haja dois buracos negros. A região está sendo representada por um grande retãngulo
cuja fronteira está orientada positivamente: o vetor perpendicular (considerado com o ângulo positivo)
aponta para o interior da região.
figura ilustra de modo "plano" uma região do Universo
em que haja dois buracos negros. A região está sendo representada por um grande retãngulo
cuja fronteira está orientada positivamente: o vetor perpendicular (considerado com o ângulo positivo)
aponta para o interior da região.
Qualquer cálculo envolvendo esta região tem que ser feito com a retirada de uma parte da região
envolvendo os dois buracos negros, o que representei com dois círculos que envolvem os polos.
Consequentemente o domínio dos cálculos que eu fizer é o retãngulo com estes dois discos retirados e
assim a fronteira da região é uma curva formada de três pedaços - uma curva que não é conexa.
Desejo mostrar que tem um sentido físico, energético, que justifica a orientação escolhida. A
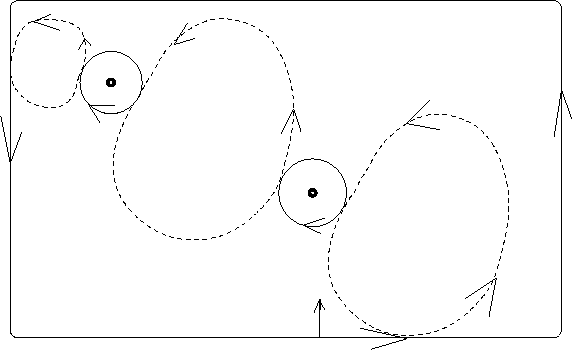 próxima figura
tem o objetivo de justificar a escolha da orientação.
próxima figura
tem o objetivo de justificar a escolha da orientação.
Pense num flúido espesso disperso nesta região,
e admita que há um movimento na fronteira, no sentido da orientação da mesma. Então este movimento na
fronteira vai ocasionar um um sentido de movimentação para o flúido disperso na região e você pode
ver a curva que uma partícula, no flúido, representada por uma das curvas fechadas que aparece na figura, e é tangente
à fronteira, irá percorrer. O movimento desta particular deve
encontrar um movimento coerente nas fronteiras internas que é o que mostra a figura.
Posso dizer que, atravez do movimento do flúido, eu induzi uma orientação nos três pedaços de que se compõe
a fronteira, os dois círculos e o retângulo externo,
a partir da orientação que eu dei ao retângulo.
Certamente, nesta questão do buraco negro uma orientação diferente deveria ser dada à fronteira dos dois
círculos interno para obedecer a à Física do problema - a presença de dois grandes atratores de gravidade,
neste caso a orientação seria a que mostra a próxima figura.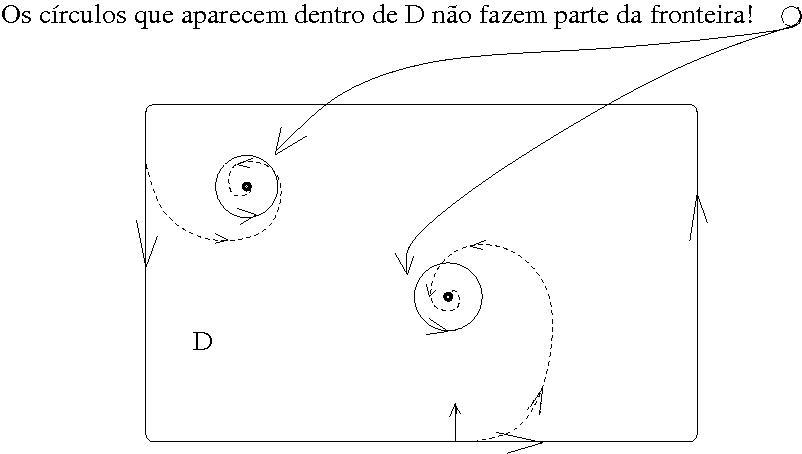
Problemas deste tipo são estudados numa disciplina chamada sistemas dinâmicos que
usa equações diferenciais como instrumento básico.
Os círculos que aparecem dentro de D não fazem parte da fronteira. Este é um problema diferente dos
descritos nas duas outras figuras. D é o retângulo retirados apenas dois pontos e qualquer "coisa" que
entrar passar pelos dois círculos indicados "com pouca velocidade", será atraido violentamente para o ponto, buraco negro.
Se não entrar, terá sua rota alterada pela atração da gravidade.
Os dois círculos, na figura, estão
apenas marcando a zona de risco...(de altíssima atração de gravidade).
Se você desenhar o vetor perpendicular em
qualquer ponto das duas espirais que aparecem na figura, ele deve se encontrar numa reta que passa próximo de
um dos buracos negros, indicando que é esta a direção sobre a qual atua a atração da gravidade.






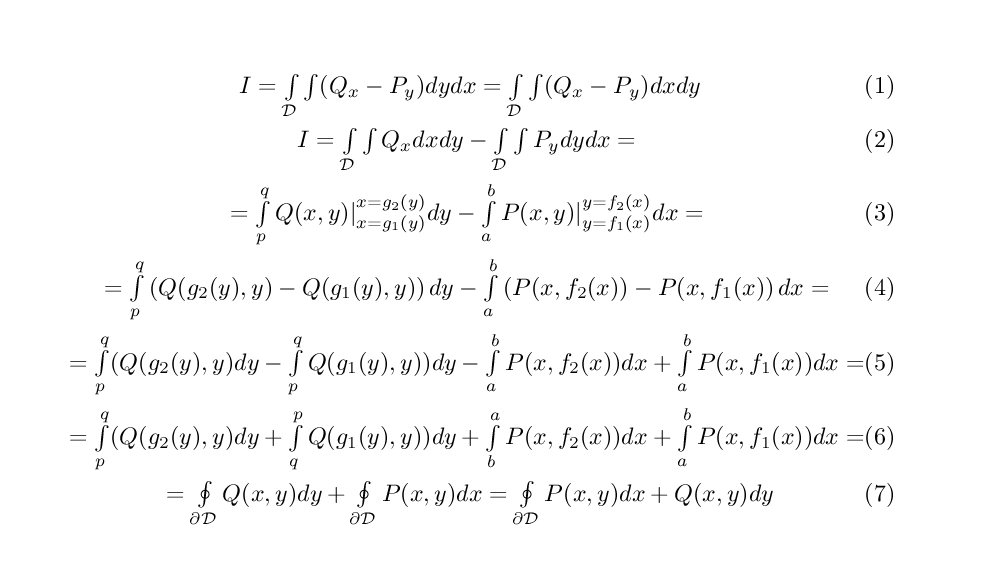


 figura ilustra de modo "plano" uma região do Universo
em que haja dois buracos negros. A região está sendo representada por um grande retãngulo
cuja fronteira está orientada positivamente: o vetor perpendicular (considerado com o ângulo positivo)
aponta para o interior da região.
figura ilustra de modo "plano" uma região do Universo
em que haja dois buracos negros. A região está sendo representada por um grande retãngulo
cuja fronteira está orientada positivamente: o vetor perpendicular (considerado com o ângulo positivo)
aponta para o interior da região.  próxima figura
tem o objetivo de justificar a escolha da orientação.
próxima figura
tem o objetivo de justificar a escolha da orientação. 