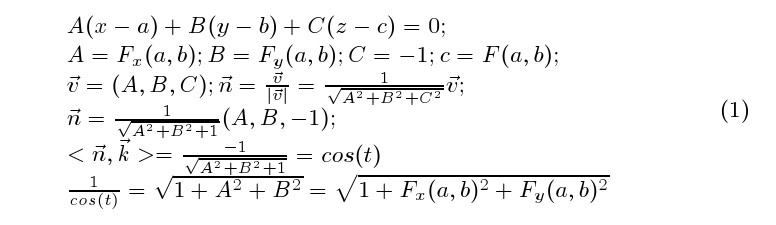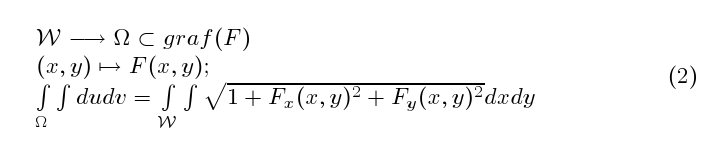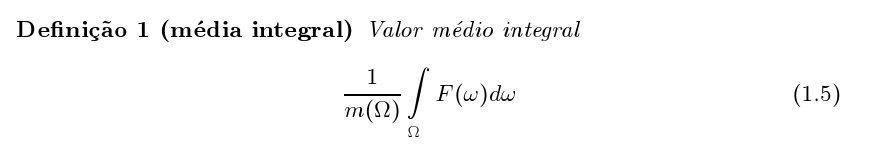palavras chave: áreas de superfícies no espaço,
centro de massa,
integral de superfície, mudança de variáveis, parametrização de
superfícies, superfície parametrizada.
Áreas de superfícies no espaço.
Uma superfície num espaço de dimensão maior do que dois, em 3D ou em dimensão
mais alta, é a imagem de uma superfície plana. A forma exata de falar é
dizer que ela pode ser parametrizada sobre uma superfície plana.
Há alguns problemas neste processo de parametrização que podem ser facilmente
observados com um exemplo bem conhecido: um mapa mundi.
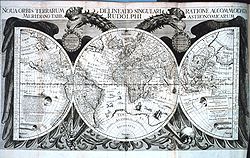Aqui você pode ver o mapa mundi feito por Kepler e visualizar o problema
que se pode ter para representar numa região retangular uma superfície, como
é o caso, que encerra um sólido do espaço - a fronteira do sólido.
Um dos problemas neste caso é a "linha do tempo" onde a esfera é aberta para
ser disposta numa região plana.
O problema menor: a área da esfera não é igual à área do retângulo que lhe
serve de conjunto de parametrização (domínio das equações paramétricas).
Da mesma forma, qualquer área de uma região representada no mapa
retangular tem uma área diferente da real região que se encontra sobre
a esfera.
A forma de entender e calcular frente a este problema fica facilmente resolvido
com a regra da cadéia que provê o coeficiente local de distorção
entre a
área no domínio de parametrização e a área na superfície
espacial. Este é o objetivo deste texto.
Há outros problemas que não vou
discutir aqui, a palavra "atlas" pode lhe servir de apoio para fazer uma busca
na Internet e ver outros problemas ligados a esta questão, e eu suponho que
você será suficientemente curios@ para ir em busca destes problemas para ver
que há mais coisas do que a simples distorção da área na representação de
uma superfície (ou de um objeto qualquer) entre espaços de dimensões
diferentes.
A lei do coseno
Vou usar uma representação geométrica simples para mostrar-lhe como
podemos descobrir o coeficiente de distorção e depois vou
mostrar-lhe como
entendê-lo dentro da expressão da regra da cadéia.
A área de uma elipse
Podemos entender uma elipse como um círculo distorcido.
Há diversas formas de distorcer um círculo, uma delas consiste em projetá-lo
sobre um plano, e o resultado será outro círculo (se os dois planos - o de saída
e o de chegada) forem paralelos.
Se estes dois planos não forem paralelos a imagem do círculo no plano de
chegada será uma elipse contida dentro de um cilindro com mesmo raio do
círculo no plano de saída. Preciso que você entenda claramente esta afirmação
porque vou precisar dela nos próximos cálculos.
O programa exer11_00_01.calc foi usado para produzir algumas
imagens para esta página, possivelmente você conseguirá entender melhor
se rodar o programa e assim ver melhor os gráficos sob a sua perspectiva.
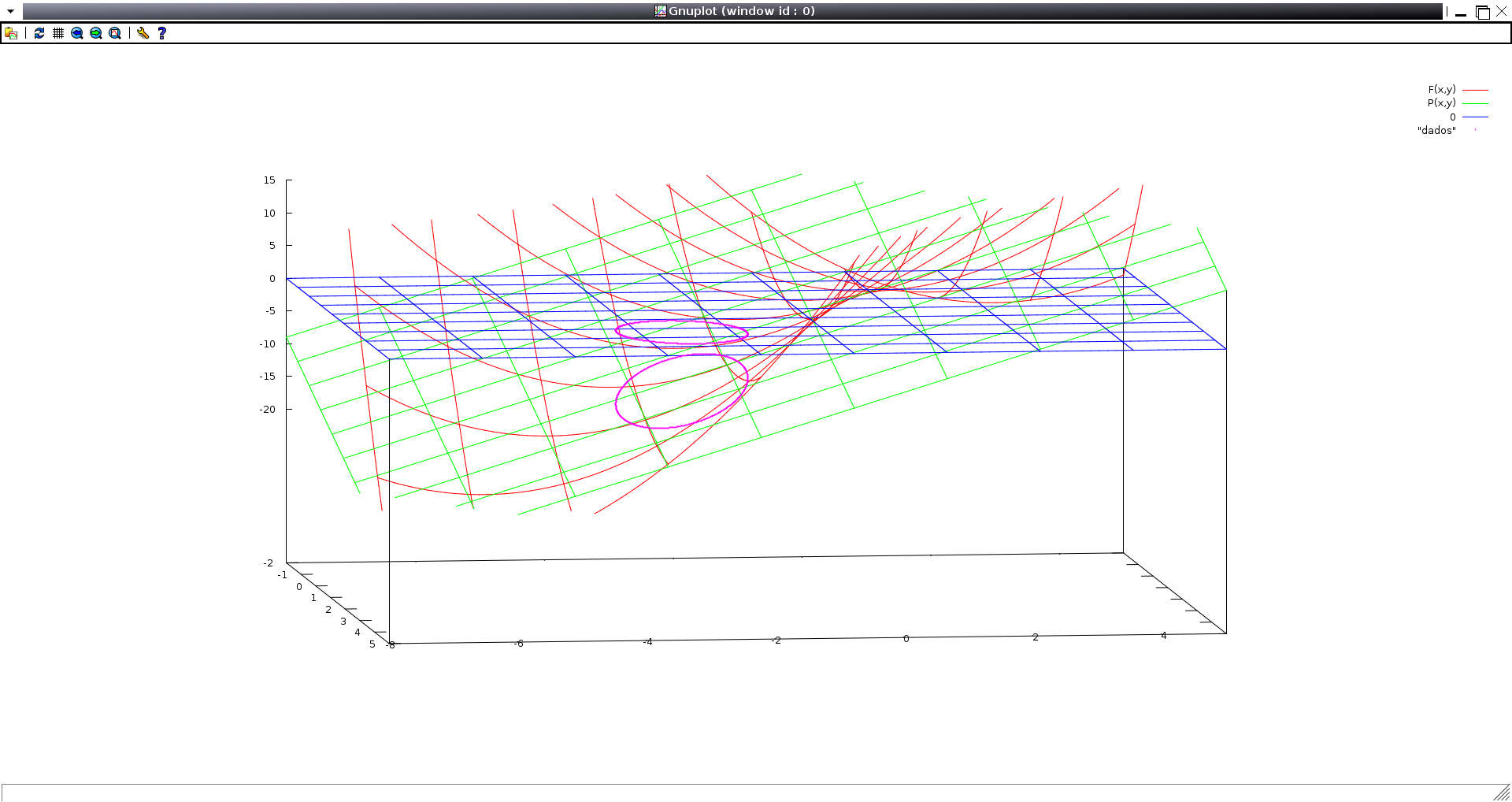
Na imagem você pode ver um círculo desenhado no plano XOY e sua
projeção (perpendicular - ao longo do eixo OZ) no plano tangente ao gráfico
de uma função.
Imagine agora um cilindro tendo por base o círculo no plano XOY.
A elipse-imagem terá o
seu eixo menor coincidente com o diâmetro do cilindro
e se expande no cilindro
para "acomodar" o eixo maior.
Para este caso, área da elipse é
(área do círculo)/cos(t)
em que t é
o ângulo entre o plano tangente e o plano XOY - logo o ângulo do vetor perpendicular
ao plano o que nos leva ao gradiente da função z = F(x,y).
Usei uma função z = F(x,y) apenas para obter mais facilmente
as imagens - rapidamente posso trocar o plano apenas indicando os
parâmetros a,b. Uma leitura do programa vai obrigá-l@ a rever tudo
o que já estudamos de Cálculo e ao mesmo mostrar-lhe que o que estudamos
é necessário se você deseja entender como se colocam imagens no espaço.
Com o programa exer11_00_01.calc você pode ver que a imagem
do círculo é uma elipse cuja área é maior que a do círculo porque o seu eixo
menor coincide com o diâmetro do cilindro. Consequentemente o coeficiente
de distorção que vai me dar a área da elipse como múltiplo da área do círculo
é maior do que 1: 1/cos(t).
Uma outra experiência simples vai lhe mostrar a mesma imagem:
você precisa
de uma lanterna e uma folha de cartolina (papel pesado).
Projete a luz no papel, quando o eixo da lanterna estiver perpendicular
ao papel, você verá uma imagem circular (maior do que o círculo da lanterna
porque você está projetando um cone de luz).
Mude o ângulo e verá
surgir uma elipse cujo eixo menor coincide com o diâmetro da imagem
do círculo anterior, e o diametro maior passa do diâmetro.
Conclusão: a área da elipse é obtida por um coeficiente maior
do que 1 porque o círculo está contido na imagem da elipse.
Uma aplicação simples
Por sorte os que mexem com corrupção imobiliária nunca irão estudar
Cálculo, e se estudarem não vão passar de Cálculo I não chegando até este
ponto.
A área de uma região montanhosa é maior do que a área de uma região
plana! Quer dizer que o preço da construção por metro quadrado tem
que ser maior na serra! Mas vai ser difícil este pessoal convencer deste
detalhe ao comprador usando a argumentação do Cálculo!
Nesta imagem, obtida com o programa exer11_00_01.calc
acho que você pode ver mais claramente que a elipse está expandida
relativamente ao círculo (se acomodando ao cilindro que tem o círculo por
base).
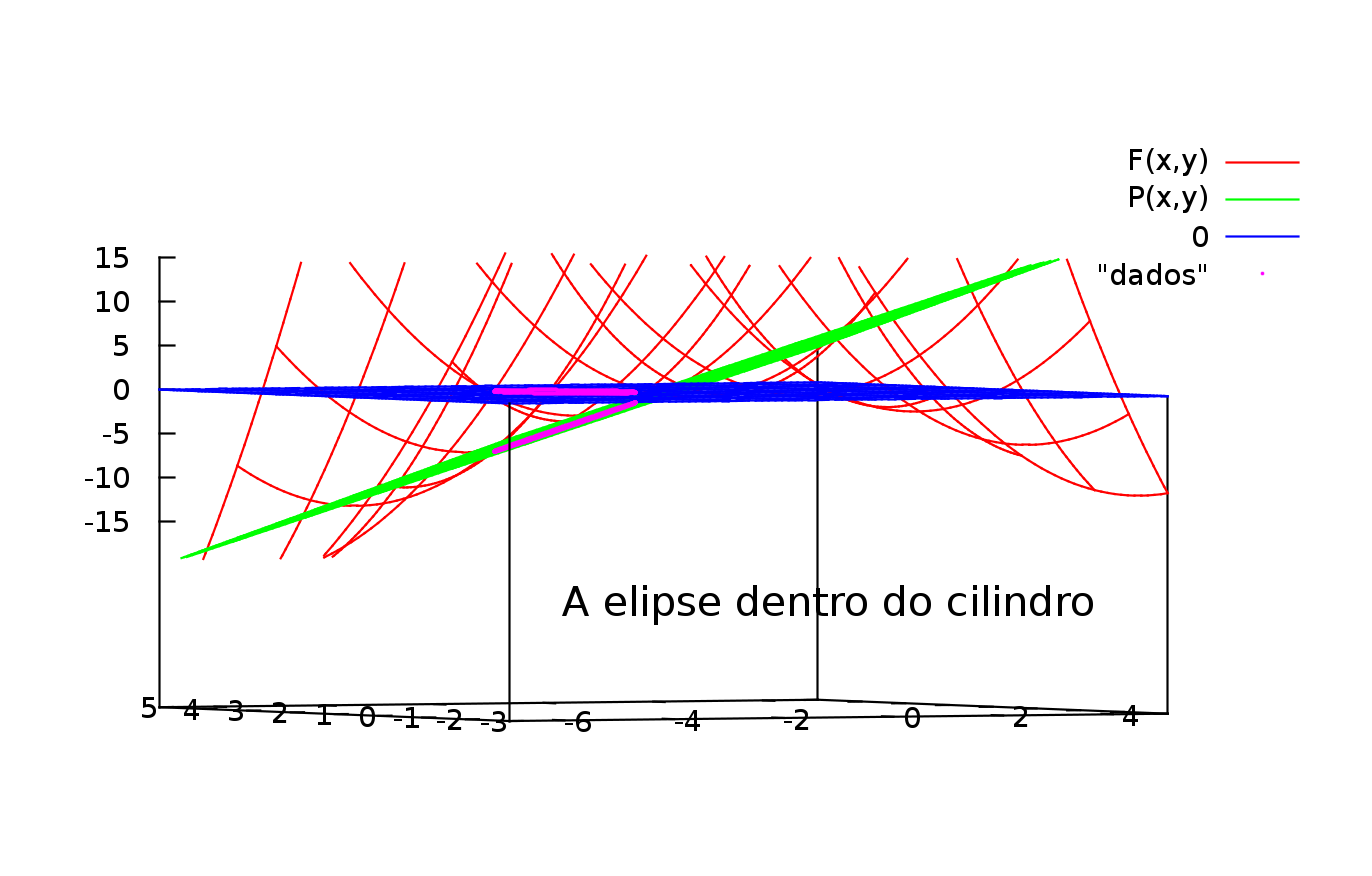Esta outra imagem mostra que a elipse ficou de tal forma dilatada que
saiu do campo da imagem projetada no programa.
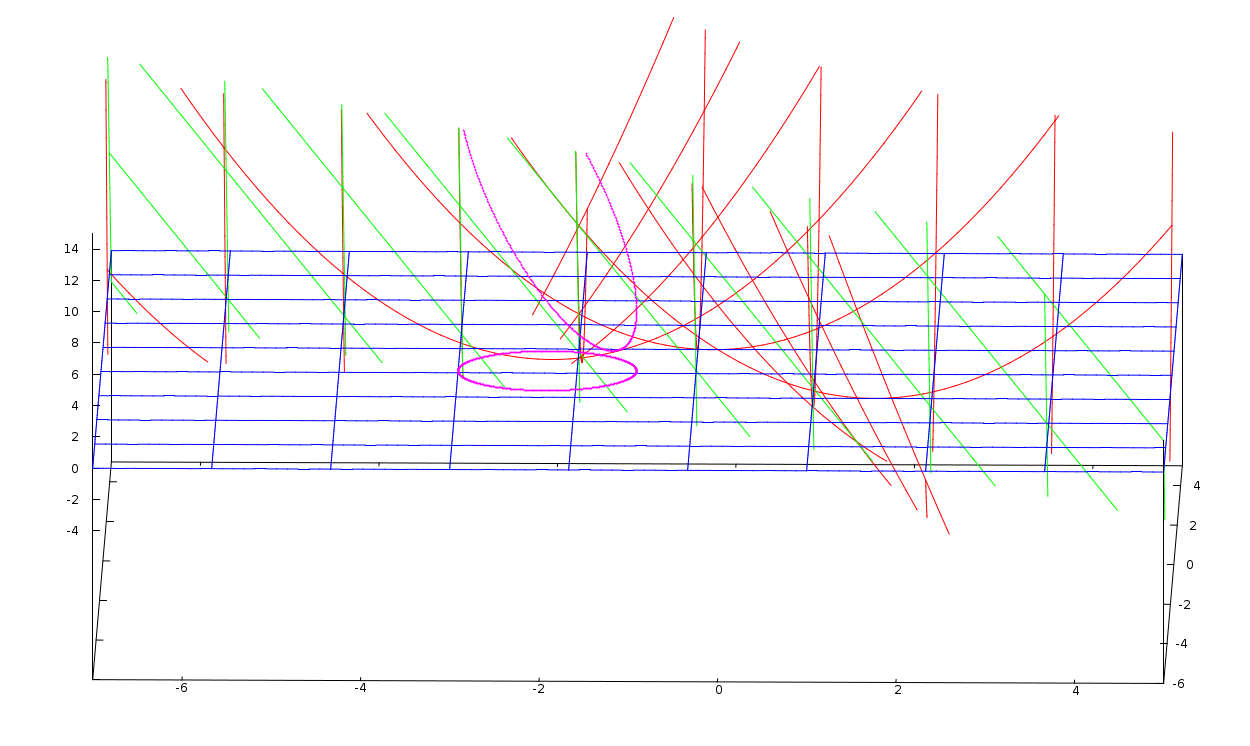
A lei do coseno - um coeficiente de distorção constante.
A lei do coseno me dá um coeficiente de distorção constante o que me
permite calcular a área de uma figura projetada num plano (uma figura
plana no espaço - obtida pela projeção de uma figura plana contida em
XOY sobre um plano que faça o ângulo t com o plano XOY.
Vou mostrar-lhe como obter a expressão da integral para o cálculo da
área da superfície que é imagem de uma região, W, do plano.
Usando a notação do programa exer11_00_01.calc
cada
passo do algoritmo pode ser descrito assim:
- escrevo a equação do plano tangente ao gráfico de F num ponto
arbitrário (a,b,c) = (a,b,F(a,b));
- posso agora obter a expressão de um vetor
perpendicular ao gráfico de z = F(x,y) neste ponto (a,b,c);
- normalizo o vetor perpendicular, calculo portanto um vetor normal
ao gráfico de F no ponto (a,b,c);
- o produto escalar do vetor normal com o vetor unitário, k, do eixo OZ
me fornece o cos(t)(a,b) o coeficiente local de distorção.
As contas são estas:
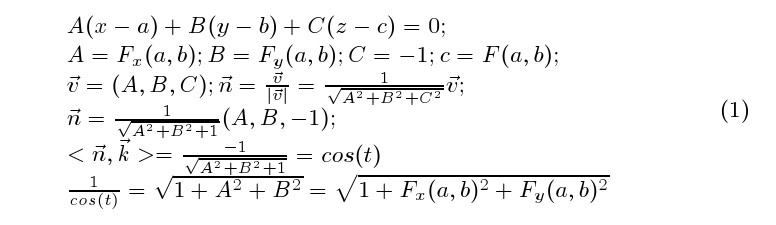
e você pode notar a semelhança com a fórmula para o cálculo do comprimento
de arco, equação (19), página 8, da lista 07.
A última expressão na equação (1) é o ``coeficiente de
deformação local'' na integral que nos permite de calcular a área da
imagem de uma região W projetada sobre a superfície graf(F). Mais
precisamente:
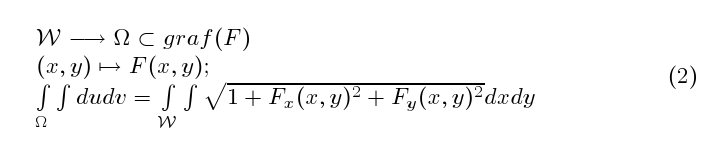
A primeira integral dupla, na última equação, é apenas um símbolo
que você pode ler "área de Omega".
Área de uma superfície parametrizada sobre W.
Vou escrever agora a expressão da integral para o cálculo dá area de
uma superfície limitada, ainda obtida como imagem de uma região W do
plano XOY - dizemos que a superfície está parametrizada em W.
Os dados do problema são:
- (u,v,w) um ponto genérico da superfície contida no R3;
- Um sistema de equações paramétricas u,v,w definidas em W;
- u = u(x,y) ; x,y em W;
- v = v(x,y) ; x,y em W;
- w = w(x,y) ; x,y em W;
Posso, por analogia aos cálculos que já fizemos na lista 07, escrever a
expressão da área de uma região limitada sobre uma superfície ${\cal S}$
quando esta superfície estiver parametrizada sobre uma região do plano.
Em geral pensamos na região do plano XOY como um retângulo ou um círculo
quando o cálculo da integral fica fácial (se soubermos calculá-la).
A expressão é da integral com equações paramétricas é
Integral como distribuição de massa
Evite de se intimidar com a "generalidade" desta último parágrafo. O objetivo
não é o de confundí-lo, mas de aguçar sua curiosidade para se
aprofundar no estudo da integração.
É uma espécie de conclusão.
Os cálculos que fiz acima nos conduzem a ver o integrando como uma
função de distribuição de uma certa "massa" no espaço. Em vez da palavra
"massa" podemos usar "energia". A integral representa a quantidade
total de algum fenômeno definido em uma certa região e pode ser expressa
com o símbolo
Centro de massa
Uma aplicação interessante no cálculo de qualquer integral são os conceitos
de valor médio, centro de massa.
Estes conceitos estão interligados e é preciso alguma prática para
ver a distinção entre eles e algumas vezes precisamos vê-los como
dois conceitos distintos.
O valor médio integral generaliza o conceito de
média ponderada.
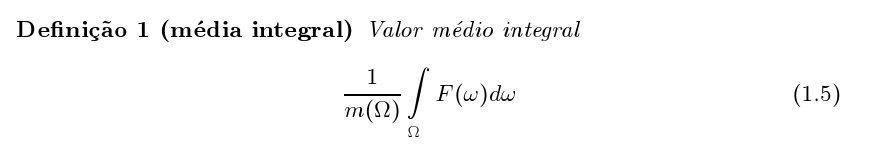
Se escrevermos uma soma de Riemann para esta integral vamos poder
identificar os pesos (cuja soma é 1) numa média aritmética ponderada,
devido a divisão pela medida do espaço.
Se a função F for vetorial (e não há nada especial em calcular uma
integral sobre funções vetoriais - como no caso de derivadas de funções
vetoriais), o resultado da integral é um vetor do espaço, portanto
uma posição.
Então a integral calculou um ponto do espaço, em vez de calcular um
número.
Se a função que estiver no integrando for constante 1,
o resultado é o centro do domínio de integração - o seu centro de massa.
Se a função no integrando for diferente de 1 podemos interpretar este
fato dizendo que o domínio de integração não tem massa uniformemente
distribuida e portanto o seu centro de massa não coincide com o seu
centro geométrico (a média integral).